Domain & Range

Domain and Range

Example 2

The function 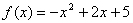FindRangeEx2-1 represents the height of a ball dependent on the time in the air. Determine the domain and range of the quadratic function.

Step 1. Determine the domain.

Since this function is modeling a situation, the label of the inputs is important. In this situation, the input values are based on time and therefore, the domain is FindRangeEx2-2 or the domain is all input greater than or equal to 0, since you cannot have negative time.

Step 2. Find the vertex.

FindRangeEx2-3

Step 3. Determine the range.

Since the graph opens down and the vertex is (-1, 4), the range should be FindRangeEx2-4. However, since -1 is not part of the input, the range will have to start at the first domain of 0. The range of the situation is FindRangeEx2-5.