Print bookPrint book

Domain & Range

Site: Farwell
Course: Michigan Algebra I Sept. 2012
Book: Domain & Range
Printed by: Guest user
Date: Sunday, November 24, 2024, 2:14 AM

Description

Domain and Range

Table of contents

Introduction

The domain for any function is the set of all input values to which the rule applies. These are called the independent variables. The range is the set of all output values. These are called the dependent variables. The domain and range can be expressed as a list of numbers, in words, or using set notation.

The domain of a quadratic function f(x) is all real numbers, unless the quadratic is modeling a situation in which there is a restriction on the input values. The range is restricted by the y -coordinate of the vertex. When the vertex is a minimum, the range will be greater than or equal to its y -coordinate and when the vertex is a maximum, the range is less than or equal to its y -coordinate.


Range

To find the range, you must find the minimum or maximum value of the function, which is going to be the vertex. If the maximum value of the function is (3, 17), then the output cannot be greater than 17. The range is all values of y such that y is less than or equal to 17, or in set notation: FindRange1. If there is a minimum value at (1, 4), then the output cannot be less than 4. The range is all values of y such that y is greater than or equal to 4, or in set notation: FindRange2.

In general, if the parabola opens upward, the range of the quadratic function

f(x) = ax2 + bx + c is, FindRange3. If the parabola opens downward, the range of the quadratic function f(x) is, FindRange4.


Example 1

Find the domain and range of the function f(x) = 2x2? 4x + 1.

Step 1. Determine the domain.

Since this function is not modeling a situation, there is no restriction on the inputs. The domain is FindRangeEx1-1 in other words, the domain is all real numbers.

Step 2. Find the vertex.

FindRangeEx1-2

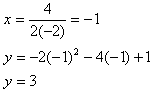
Step 3. Determine the range.

Since the graph opens up and the vertex is (-1, 3), the range is FindRangeEx1-3 or the set of all y-values that are greater than or equal to 3.


Example 2

The function FindRangeEx2-1 represents the height of a ball dependent on the time in the air. Determine the domain and range of the quadratic function.

Step 1. Determine the domain.

Since this function is modeling a situation, the label of the inputs is important. In this situation, the input values are based on time and therefore, the domain is FindRangeEx2-2 or the domain is all input greater than or equal to 0, since you cannot have negative time.

Step 2. Find the vertex.

FindRangeEx2-3

Step 3. Determine the range.

Since the graph opens down and the vertex is (-1, 4), the range should be FindRangeEx2-4. However, since -1 is not part of the input, the range will have to start at the first domain of 0. The range of the situation is FindRangeEx2-5.


Video Lesson

To learn how to find domain and range of a quadratic function, select the following link:

Domain and Range

Practice

Domain and Range Worksheet

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Key

Domain and Range Answer Key

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

"Domain and Range." http://hotmath.com/help/gt/genericalg1/ section_9_3.html (accessed 7/13/2010).

Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project

Holt, Rinehart & Winston, "Finding Maximums and Minimums." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.html?contentSrc=7096/7096.xml (accessed 8/22/2010).