Absolute Value
Absolute Value Functions
Solving by Graphing
Absolute value equations can be solved by graphing as well as algebraically. Suppose the given equation is 3 Ix + 5I - 2 = 10. Graph the left side of the equation and the right side separately and calculate where the two graphs intersect. The intersection points of the two graphs are the solutions of the original equation.
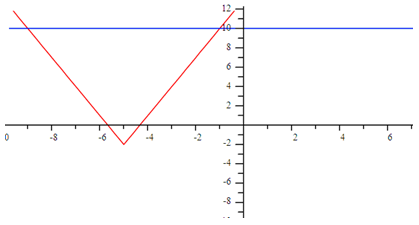
You can see by the graph that there are two solutions, where the red and blue graphs intersect. This is something absolute value functions also have in common with quadratics. In this case, the solutions are x = -1 and x = -9 which can be verified by solving algebraically.