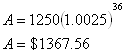Print bookPrint book

Compound Interest

Site: Farwell
Course: Michigan Algebra I Sept. 2012
Book: Compound Interest
Printed by: Guest user
Date: Thursday, November 21, 2024, 10:16 PM

Description

Compound Interest

Table of contents

Formula

One very important application of exponential functions is compound interest. Below is the formula:

CompoundInterest

A is the ending amount

P is the beginning amount (or "principal")

r is the interest rate (expressed as a decimal)

n is the number of times the loan is compounded in one year

t is the total number of years

*Note: The formula is set up this way because interest rates are generally reported as annual interest rates.

Example 1

You are investing $1250 into an account that yields3%, compounded monthly, and you plan to invest for a total of 3 years. How much money will you have at the end of the three years?

Step 1. Identify the variables.

A is the ending amount, this is what you are trying to determine.

P is the beginning amount, in this case $1250.

r is the interest rate written in the form of a decimal, in this case 0.03.

t is the time in years, in this case 3 years.

n is the number of times compounded per year, in this case it is being compounded monthly and therefore n = 12.

Step 2. Substitute the variables into the formula.

CompoundIntEx1-1

Step 3. Calculate the formula, you may need a calculator.

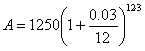
Example 2

Suppose that you plan to need $10,000 in thirty-six months' time when your child starts attending college. You want to invest in an instrument yielding 3.5% interest, compounded monthly. How much should you invest?

Step 1. Identify the variables.

A is the ending amount, in this case $10,000.

P is the beginning amount, this is what we are trying to determine.

r is the interest rate written in the form of a decimal, in this case 0.035.

t is the time in years, in this case CompoundIntEx2-1 years.

n is the number of times compounded per year, in this case it is being compounded monthly and therefore n = 12.

Step 2. Substitute the variables in to the formula.

CompoundIntEx2-2

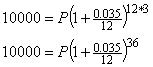
Step 3. Calculate the formula, you may need a calculator.

CompoundIntEx2-3

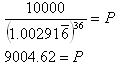
You need to invest about $9004.62.

Example 3

Peter earned $1500 last summer. If he deposited the money in a bank account that earns 5% interest compounded yearly, how much money will he have after five years?

Step 1. Identify the variables.

A is the ending amount, this is what we are trying to determine.

P is the beginning amount, in this case 1500.

r is the interest rate written in the form of a decimal, in this case 0.05.

t is the time in years, in this case 5 years.

n is the number of times compounded per year, in this case it is being compounded yearly and therefore n = 1.

*Note: Since n = 1, it will not effect the equation and can be eliminated from the formula. In this case the general form of an exponential function ( y = abx) is just as effective at solving the problem.

Step 2. Substitute the variables into the formula.

CompoundIntEx3-1

Step 3. Calculate the formula, you may need a calculator.

y = 1500 · (1.05)5 = $1914.42

.

Video Lessons

To learn how to determine compound interest, select the following link:

Compounded Quarterly

Compound Interest

Guided Practice

To solidify your understanding of compound interest, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.

Guided Practice

Practice

Compound Interest Worksheet

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Key

Compound Interest Answer Key

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

Gloag, Anne & Andrew. "Exponential Functions." February 24, 2010.

http://www.ck12.org/flexr/chapter/4478

Holt, Rinehart, & Winston. "Exponential & Radical Functions."

http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch11_03_homeworkhelp.html (accessed September 11, 2010)

Stapel, Elizabeth. "Exponential Functions: Compound Interest." Purplemath. Available from http://www.purplemath.com/modules/expofcns4.htm . (accessed 11 September 2010)