Print bookPrint book

Domain & Range

Site: Farwell
Course: Michigan Algebra I Sept. 2012
Book: Domain & Range
Printed by: Guest user
Date: Thursday, November 21, 2024, 10:57 PM

Description

Domain & Range

Table of contents

Introduction

As discussed previously, for exponential functions of the form, Domain, there is no restriction on the value of x. Therefore, the function is defined for all real values of x, and the domain is Domain2.

All exponential functions have an asymptote, or line that the graph will approach but never touch or cross. Therefore, the range of an exponential function of the form, Range, is dependent on the sign of a and the value of the asymptote. If a is a positive value then the graph will approach the asymptote from the top, which means the range will be greater than the asymptote. If a is negative, then the graph will approach the asymptote from the bottom, which means the range will be less than the asymptote. Because the graph never intersects the asymptote, the range will never include this value.


Example 1

Find the domain and range of the function: g(x) = 3.2x+1 + 2.

Step 1. Find the domain.

Since the function is not representing a situation, the x can be any real number.

Therefore, the domain is DREx1-1.

Step 2. Find the range.

This graph is shifted up 2 and has an asymptote at the line y = 2. It also has a positive a-value.

Therefore, the range of the function is DREx1-2.

Example 2

Find the domain and range of the function: DREx2-1.

Step 1. Find the domain.

Since the function is not representing a situation, the x can be any real number.

Therefore, the domain is DREx2-2.

Step 2. Find the range.

This graph is shifted to the right 2, which does not affect the asymptote. It has an asymptote at y = 0. It also has a positive a-value.

Therefore, the range of the function is DREx2-3.

Example 3

Find the domain and range of the function: DREx3-1.

Step 1. Find the domain.

Since the function is not representing a situation, the x can be any real number.

Therefore, the domain is DREx3-2.

Step 2. Find the range.

This graph is shifted down 2 and has an asymptote at y = -2. It also has a negative a-value.

Therefore, the range of the function is DREx3-3.


From a Graph

To find domain and range of an exponential function by looking at a graph, determine where the x and y-values of the graph are bounded. For domain, look at the graph and find what values of x will be included in the graph. For range, look at the graph and find what values of y are included in the graph.

DRGraph1-1

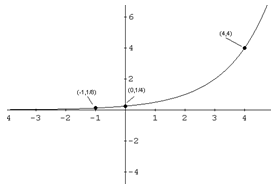
In the graph above, since all x values appear to be present in the graph, the domain is all real numbers or DRGraph1-2. Since the horizontal asymptote is y = 0, there will not be any values below, or at, y = 0. The range is y > 0, or DRGraph1-3 .

Example

Find the domain and range of the graph below.

DRGraphEx1-1

Step 1. Find the domain.

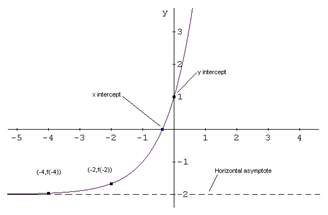
Since all x values appear to be present in the graph, the domain is all real numbers, or DRGraphEx1-2.

Step 2. Find the range.

Since the horizontal asymptote is y = -2, then there will not be any values below, or at, y = -2. The range is y > -2, or DRGraphEx1-3.

Video Lesson

To learn how to determine the domain and range of an exponential function, select the following link:

Practice

Domain & Range of Exponentials Worksheet

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Key

Domain & Range of Exponentials Answer Key

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

Adams, R., & Free High School Science Texts.2009. Exponential Functions and Graphs - Grade 11. Connexions, July 29, 2009. http://cnx.org/content/m30856/1.1/.

Dendane, Dr Abdelkader, Ph.D. "Graph of Exponential Functions." November 25, 2007.http://www.analyzemath.com/Graphing/GraphExponentialFunction.html

Khan, Salman. "Identifying Exponential Models."

http://www.khanacademy.org/video/identifying-exponential-models (accessed September 11, 2010).