Solving Equations
| Site: | Farwell |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Solving Equations |
| Printed by: | Guest user |
| Date: | Friday, December 19, 2025, 9:14 AM |
Description
Introduction
There are many forms of radical equations. However, solving them uses the same set of steps. This book will show the increasing levels of complexity of solving radical equations. This set of steps includes:
- Isolate the radical or power expression.
- Use inverse operations to eliminate the radical or power.
- Solve the remaining equation.
- Some situations will require checking for extraneous solutions.
Basic Equations
Example Solve ![]() .
.
Step 1. Isolate the radical or power expression.
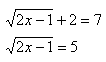
Step 2. Use inverse operations to eliminate the radical or power.
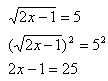
Step 3. Solve the remaining equation.
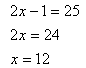
Video Lesson
To learn how to solve basic radical equations, select the following link:
Radicals on Both Sides
Example Solve ![]() .
.
Step 1. Isolate the radical or power expression.
These terms are isolated.
Step 2. Use inverse operations to eliminate the radical or power.
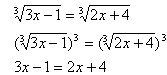
Step 3. Solve the remaining equation.
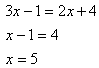
Video Lesson
To learn how to solve equations with radicals on both sides, select the following link:
Extraneous Solutions
Sometimes when solving math problems the process of simplifying creates a different domain than the original equation. This creates an invalid solution known as extraneous. An extraneous solution is the solution of the simplified form of an equation that does not satisfy the original equation and needs to be eliminated.
It is necessary to check for extraneous solutions when the original equation has a restricted domain. The equation in the next example contains a square root. Since even root functions are restricted to values greater than or equal to zero, any equation involving even roots or their corresponding fractional exponent should be checked for extraneous solutions.
There are other functions that require checks of extraneous solutions, but those will be discussed in other courses.
Example
Solve ![]()
Step 1. Isolate the radical or power expression.
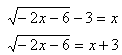
Step 2. Use inverse operations to eliminate the radical or power.
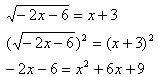
Step 3. Solve the remaining equation.
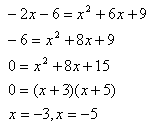
Step 4. Check for extraneous solutions.

The solution is x = -3.
Video Lesson
To learn how to solve equations with extraneous solutions, select the following link:
Rational Exponents
Example Solve ![]() .
.
Step 1. Isolate the radical or power expression.
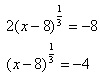
Step 2. Use inverse operations to eliminate the radical or power.
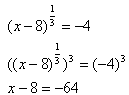
Step 3. Solve the remaining equation.
![]()
*Note: This is an odd root; therefore there is no need to check for extraneous solutions.
Video Lesson
To learn how to solve equations with rational exponents, select the following link:
Guided Practice
To solidify your understanding of solving radical equations, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
Solving Radical Equations Worksheet
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Solving Radical Equations Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Holt, Reinhart & Winston, "Rational and Radical Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch08_08_homeworkhelp.html (accessed 1/8/2011).Â
Holt, Reinhart & Winston, "Solve radical equations and inequalities." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.html?contentSrc=8151/8151.xml (accessed 1/8/2011).