Remaining Power Rules
| Site: | Farwell |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Remaining Power Rules |
| Printed by: | Guest user |
| Date: | Sunday, February 1, 2026, 5:00 AM |
Description
Power of a Power
To simplify an expression that has an exponent raised to a power, multiply the existing exponent by the power.
Power of a Power Rule : (xn)m = xn·m
To see why this rule works, see the expansion below:
![]()
Therefore, ![]() .
.
Example
Simplify ![]() .
.
Use the Power of a PowerRule to multiply the exponents.
![]()
Video Lesson
To see a video lesson about how to raise a power to a power, select the following link:
Power of a Product
When a product is inside the parentheses and a power is on the outside of the parentheses, then the outside power multiplies the exponent of each element inside.
Power of a Product Rule:![]()
*Note: This rule applies to a product only. If there is a sum or difference inside, refer to the steps of multiplying binomials.
Example 1 Simplify the following expression: (x2y)4
Step 1. Rewrite the expression with each element inside the parentheses to the power on the outside.
![]()
Step 2. Use the Power of a Power Rule.
![]()
Example 2 Simplify ![]() .
.
Use the Power of a Product Rule to simplify the expression.
![]()
Example 3
Simplify ![]() .
.
Step 1. Use the Power of a Product Rule to simplify the expression.
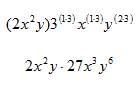
Step 2. Use the Product of a Power Ruleto simplify the expression.
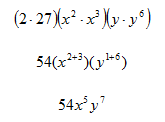
Video Lesson
To see a video lesson about how to raise a product to a power, select the following link:
Guided Practice
To solidify your understanding of power of a product, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Power of a Quotient
When the elements of a quotient have exponents and the quotient is raised to a power, then the power multiplies the exponent of each element in the quotient.
Power of a Quotient Rule : 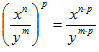 .
.
Example 1
Simplify the expression: ![]() .
.
Step 1. Use the Power of a Quotient Rule.
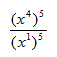
Step 2. Use the Power of a Power Rule to simplify the resulting expression.
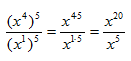
Step 3. If the bases are the same, use the Quotient of a Power Rule for Exponents to simplify the resulting expression.
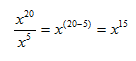
Example 2
Simplify the expression: 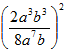 .
.
Once familiar with the rules, the order of use will become apparent when simplifying expressions.
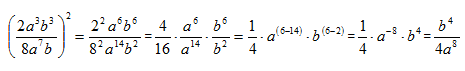
Video Lesson
To see a video about how to raise a quotient to a power, select the following link:
Guided Practice
To solidify your understanding of raising a quotient to a power, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Power of a Quotient Answer Key
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Gloag, Andrew & Anne. "Exponential Functions. "http://www.ck12.org/flexr/
chapter/4478 (accessed August 31, 2010)
Holt, Rinehart, & Winston. "Exponents and Polynomials."http://my.hrw.com/
math06_07/nsmedia/homework_help/alg1/alg1_ch07_03_homeworkhelp.html (accessed September 1, 2010).
Holt, Rinehart, & Winston. "Exponents and Polynomials."http://my.hrw.com/
math06_07/nsmedia/homework_help/alg1/alg1_ch07_04_homeworkhelp.html (accessed September 1, 2010).