Characteristics
| Site: | Farwell |
| Cours: | Michigan Algebra I Sept. 2012 |
| Book: | Characteristics |
| Printed by: | Invitado |
| Date: | samedi, 14 février 2026, 09:46 |
Description
Introduction
The following definitions are terms that will be used in this unit:
A polynomial is composed of multiple terms added together that contain only positive integer exponents. Polynomials will not have variables in the denominator. Coefficients must be real numbers.
A term is a number or the product of a number and one or more variables.
A variable is the unknown quantity represented by a letter.
A constant is a number without a variable.
A coefficient is the number in front of the variable in each term. If there is a subtraction sign, then the coefficient after the sign is negative.
The coefficient on the leading term is called the leading coefficient. In the polynomial, -3x2 + x - 4, the leading coefficient is -3.
The degree of a polynomial is the degree of the term with the greatest exponent. The polynomial, -3x2 + x - 4, is a second degree polynomial because the squared term is the largest exponent.
Examples of Polynomials
Linear and quadratic equations are examples of polynomials. These were studied in earlier units. The following are also examples of polynomials:
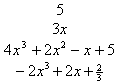
Notice that the terms are written in descending order of the variables' exponents. The polynomial, 4x3 + 2x2 - x + 5, has four terms. The coefficient of 4x3 is 4, the coefficient of 2x2 is 2, the coefficient of -3x is -3, and the constant is 1.
Non-examples
These are not polynomials:
3x2 - 2x-2 is not a polynomial because it has a negative exponent.
![]() is not a polynomial because it has a variable under the square root.
is not a polynomial because it has a variable under the square root.
![]() is not a polynomial because it has a variable in the denominator of a fraction.
is not a polynomial because it has a variable in the denominator of a fraction.
![]() is not a polynomial because it has a fractional exponent.
is not a polynomial because it has a fractional exponent.
Classifications
Polynomials are classified by their number of terms and by their degrees.
There are special names for polynomials with 1, 2 or 3 terms:

There is also quadrinomial (4 terms) and quintinomial (5 terms), but those names are not often used. Usually, when a polynomial has four or more terms, it is usually just called a polynomial.
When a term has multiple variables, the degree of the term is the sum of the exponentswithin the term. For example, the term 3x3y2z is a 6th degree or order because the exponents add to 6 (3 + 2+ 1).
Degrees
Polynomials are also classified by the degree of the largest exponent as follows:
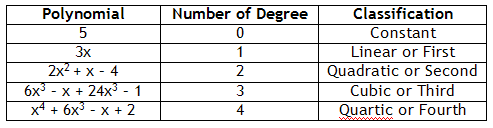
Polynomials with larger degrees are named by the number of the degree:
6x5 Fifth degree
-x6 Sixth degree, etc.
Example: Give the degree of the following polynomial: 2x5 - 5x3 - 10x + 9
This polynomial has four terms, including a fifth-degree term, a third-degree term, a first-degree term, and a constant term.
This is a fifth-degree polynomial.
Guided Practice
To solidify your understanding of polynomial identification, visit the following links.
The Hotmath.com site provides interactive practice with answers available. Click "view solution" to check your work. Click the arrows on the bottom red bar to help with the problem, or use one of the other options below for additional help.
The Holt, Rinehart and Winston Homework Help Online link provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Evaluating
Because polynomials fit the definition of a function, [for every input (x-value) there is exactly one output (y-value)] function notation can be used. Instead of writing y = x4 + 6x3 - x + 2, in function notation it would be written P(x) = x4 + 6x3 - x + 2. The letter, P, is often used for polynomial functions.
Evaluating a polynomial is the same as evaluating linear or quadratic functions: substitute the given value of x, and find the value for y.
Example Evaluate P(x) = 2x3 - x2 - 4x + 2, when x = -3.
Step 1. Substitute "-3" for the "x", remembering to be careful with parentheses and the negatives:
P (-3) = 2(-3)3 - (-3)2 - 4(-3) + 2
Step 2. Simplify the expression.
2(-27) - (9) + 12 + 2
-54 - 9 + 14
-63 + 14
-49
P (-3) = -49
Guided Practice
For guided practice in evaluating polynomials, select the following link and complete problems #1 - 11:
Simplifying
Combining like terms is a necessary skill to have when working with polynomials. In order to write a polynomial in simplest form, all like terms need to be combined. Terms can be combined when they have the exact same variable. Here are some examples:
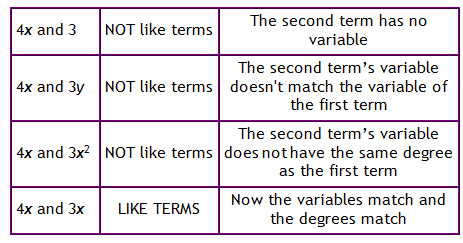
Examples
Example 1 Simplify 3x + 4x.
Step 1. First determine whether the terms are like terms and can be combined.
These are like terms since they have the same variable.
Step 2. Combine the terms by adding the coefficients.
3x + 4x = (3 + 4)x = 7x
Example 2 Simplify 2x2 + 3x - 4 - x2 + x + 9.
Step 1. Group like terms together.
2x2 + 3x - 4 - x2 + x + 9
(2x2 - 1x2) + (3x + 1x) + (-4 + 9)
Step 2. Simplify.
x2 + 4x + 5
Guided Practice
To solidify your understanding of simplifying polynomials, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Simplifying Expressions
Before evaluating any algebraic expression, simplify it. This will make all calculations easier. Here are the basic steps to follow to simplify any algebraic expression including polynomials:
Step 1. Remove parentheses by multiplying factors.
Step 2. Use exponent rules to remove parentheses in terms containing exponents.
Step 3. Combine like terms by adding coefficients.
Step 4. Combine the constants.
Example 1
Simplify the following expression.
![]()
Step 1. Remove parentheses by multiplying factors.
![]()
Step 2. Use exponent rules to remove parentheses in terms containing exponents.
![]()
Step 3. Combine like terms by adding coefficients.
![]()
Step 4. Combine the constants.
![]()
Example 2
Simplify the following:
x2 + 4x + 3 - 2x + 5x2 -7
Step 1. Remove parentheses by multiplying factors.
There are no parentheses.
Step 2. Use exponent rules to remove parentheses in terms containing exponents.
There are no parentheses.
Step 3. Combine like terms by adding coefficients.
x2 + 5x2+ 4x - 2x+ 3 -7
Step 4. Combine the constants.
6x2 + 2x - 4
Practice
Simplifying Polynomials Worksheet
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
"Adding and Subtracting Polynomials." http://algebra-tutoring.com/polynomials-3.htm (accessed 08/12/2010).
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Exponents and Polynomials ." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/
alg1_ch07_05_homeworkhelp.html (accessed 9/7/2010).
Holt, Rinehart & Winston, "Polynomials ." http://my.hrw.com/math06_07/nsmedia/homework_help/msm3/msm3_
ch14_02_homeworkhelp.html (accessed 9/7/2010).
Hot Math, "Practice Problems." http://hotmath.com/help/gt/ genericalg1/section_6_3.html (accessed 08/09/2010).
Math Is Fun, "Monomials, Binomials, Trinomials." http://www.mathsisfun.com/ algebra/polynomials.html (accessed 08/09/10).
Math.com, "Simplifying." http://www.math.com/school/subject2/lessons/S2U2L5DP.html (accessed 08/21/2010).
"Naming Polynomials." http://www.kutasoftware.com/free.html (accessed 8/10/10).
Purple Math, "Polynomials: Definitions/Evaluation." http://www.purplemath.com/modules/polydefs.htm (accessed 08/10/2010).